머신러닝을 위한 Probability and Distribution 알아보기

Probability

확률이라는 하는 것이 결국 MAP, MLE를 통해 알아본 근간이기 때문에 확률에 대해서 알아 볼 필요가 있습니다.

$\Omega$라는 세상의 모든 사건들 중에 $E_1$이라는 사건과 $E_2$라는 사건이 발생한다고 가정을 한다면 이렇게 $E_1$과 $E_2$가 발생할 수 있는 확률이라는 것이 무엇인지 정의 해보는 것 입니다. 그것을 다음과 같이 정의해보겠습니다.

$P(E) \in R$ 함수 모양을 하고 있는데 함수의 인자로 E(Event)가 들어가는 것 입니다. 함수에 E를 넣었더니 그 결과값은 R이라고 하는 continuous value가 나오고 그 값은

$P(E) \geq 0$ 이라는 것 입니다.

그리고 또 다른 제약 조건이 있는데 $\Omega$라는 이 세상의 삼라만상 모든 발생할 수 있는 확률을 다 더하면 1이 된다는 것 입니다.

$P(\Omega) = 1$

이렇게 정의하고 나면 몇가지 특성을 알아볼 수 있습니다. 예를 들면 A와 B라는 사건이 있는데 A와 B가 특수한 관계에 있는 사건이라 합시다. B라고 하는 것이 조금 더 광범위한 사건이고 A라고 하는 것이 조금 더 작은범위라고 하면

$if$ $A \subseteq B$ $then$ $P(A) \leq P(B)$ 와 같이 정의할 수 있습니다.

그리고 $P(\phi) = 0$라는 NULL 값이 존재합니다.

개별 이벤트 $P(E)$의 값은 $0 \leq P(E) \leq 1$의 조건을 만족하게 됩니다.

뿐만 아니라 집합이론과도 연관되어 있기 때문에 $P(A\cup B) = P(A) + P(B) - P(A\cap B)$와 같이 됩니다.

그리고 E가 아닌 것은 $P(E^C) = 1 - P(E)$와 같습니다.

Conditional Probability

여기까지 정의가 되고나면 조건부확률을 정의할 수 있습니다. $\Omega$가 모든 이벤트를 담고 있다면 $\Omega$안에서 범위를 주어서 범위안에서 사건이 발생할 확률을 보는 것 입니다. 예를 들어 다음과 같은 조건을 주겠습니다.

$P(A|B) = {P(A\cap B)\over P(B)}$ B라고 하는 조건이 참인 내부에서 A가 발생할 확률이 무엇인가 입니다. B라고 하는 범위 내부에서 A가 발생할 확률을 말하는 것입니다. 여기까지가 조건부 확률이고 조건부 확률을 정의하고 나면 몇가지 재밌는 공식이 있는데 그 중 아주 많이 활용하는 공식은 다음과 같습니다.

$P(B|A) = {P(A|B)P(B) \over P(A)}$

여기까지 하면은 P라고 하는 함수에 대해서 여러가지 특성을 정의해보았습니다. 그럼 P라고 하는 매핑자체에 대해서 좀 더 잘 정의해볼 필요가 있습니다.

Probability Distribution

Probability Distribution이라는 것은 어떤 이벤트가 발생한다고 하는 것은 assign하는 것입니다.

$f(x) = {e^{-{1 \over 2}x^2 } \over \sqrt{2 \Pi}}$ f는 Probability Distribution function이 되겠고 x라고 하는 것은 아까 들어왔던 E가 됩니다. "x가 1이다", "x가 2이다", "x가 3이다"와 같은 다양한 포인트를 잡아서 이벤트라고 할 수 있습니다.

probability density function

cumulative distribution function

 

Normal Distribution

다양한 정의들이 있을 수 있습니다. 그렇게 다양하게 만들어 내는 방법은 크게 두가지가 있습니다. 함수의 공식을 정해놓고 파라미터를 바꾸는 방법 그리고 함수 자체를 바꾸는 방법입니다.

Normal Distribution

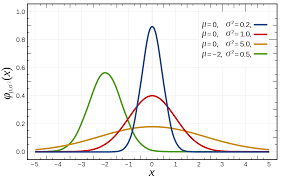
$f(x; \mu , \sigma)= {1 \over \sigma\sqrt{2 \pi}}e^{-{(x-\mu)^2 \over 2 \sigma^2}}$

Notation: $N = (\mu, \sigma^2)$

Mean: $\mu$

Variance: $\sigma$

여기서 f는 Normal Distribution의 formula고 Mean과 Variance는 parameter가 됩니다. Normal Distribution은 Long tail이 존재합니다.

Beta Distribution

Beta Distribution은 범위가 정해져 있습니다. 0~1 사이의 범위가 정해져 있기 때문에 확률을 모델링할 때 Beta Distribution을 쓸 수 있습니다. Beta Distribution의 formula는 다음과 같습니다.

$f(\theta \alpha , \beta)= {\theta^{\alpha-1} (1-\theta)^{\beta -1} \over B(\alpha, \beta) }$

$B(\alpha, \beta) = {\Gamma(\alpha)\Gamma(\beta) \over \Gamma(\alpha + \beta)}$

$\Gamma(\alpha) = (\alpha - 1)!, a \in N^+$

Notation: Beta($\alpha, \beta$)

Mean: ${\alpha \over \alpha + \beta }$

Variance: $\alpha\beta \over (\alpha + \beta)^2 (\alpha + \beta + 1)$

파라미터는 알파와 베타가 됩니다.

Binomial Distribution

$f(\theta n, p)= {n \choose k} P^k (1-p)^{n-k}$

${n \choose k} = {n! \over k!(n-k)!}$

Notation: $B(n, p)$

Mean: $np$

Variance: $np(1-p)$

p라는 것과 n이라는 것이 파라미터가 됩니다. Binomial Distribution은 이산적인 이벤트에 대해서 확률을 정의할 때 쓰게 됩니다.

 

Multinomial Distribution

Binomial Distribution은 두개 앞 뒤 두가지 케이스만 있다면 앞 뒤 옆 등 여러개의 선택지가 필요하다면 Multinomial Distribution를 쓰게 됩니다. Binomial Distribution을 특수한것 이라고 보면 됩니다.

$f(x_1, ..., x_k; n, p_1, ..., p_k) = {n! \over x_1!...x_k!} p_1^{x_1}···p_k^{x_k}$

Notation: $Mult(P), P =< P_1, ..., P_k >$

Mean: $X(E_i) = np_i$

Variance: $Var(x_i) = np_i(1-p_i)$

 

 

이외에도 포아송 분포등 여러가지 분포가 있지만 머신러닝을 공부하는데 있어 위의 분포만 알고 있어도 큰 도움이 됩니다.

 

출처: https://www.youtube.com/watch?v=oNTXMgqCv6E&list=PLbhbGI_ppZISMV4tAWHlytBqNq1-lb8bz&index=6

 

이미지출처 : https://machinelearningmastery.com/continuous-probability-distributions-for-machine-learning

이미지출처 : https://ko.wikipedia.org